Can you count the number of triangles in the given figure
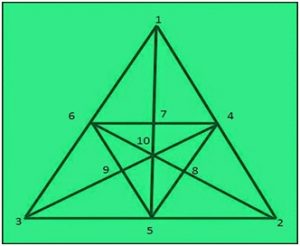
Solution: There are multiple solutions to solving the puzzle. Let us first number the vertices as shown. Using the approach of Problem Solving, first break down the problem into smaller parts -Decomposition.
Let us begin with counting the number of triangles in three triangles – 1-2-10, 2-3-10 and 3-1-10.
First consider 1-2-10: It has two identical triangles 1-4-10 and 2-4-10.
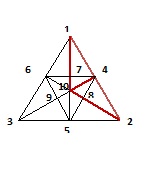
Number of triangles in 1-4-10 is 1-4-7,1-4-10,7-4-10 = 3
So total number of triangles in 1-2-10 = 3 * 2 + 1 = 7
Similarly for 2-3-10 & 3-1-10 we have 7 triangles each , hence a total = 7*3 = 21
Now we will count triangles in 1-2-10 and 2-3-10 but not already counted before. That is they do not belong entirely to 1-2-10 or 2-3-10 but cut across the two. These are –
3-4-2, 3-4-5, 9-4-5,1-5-2, 1-5-4, 2-5-4,5-4-10, 5-7-4 = 8
Similarly for 2-3-10 & 3-1-10 and 3-1-10 and 1-2-10. So we have 8*3 = 24
Finally consider triangles that cut across all three in 1-2-10,2-3-10 and 3-1-10 but have not been counted before. That is they are not entire in one or two of these triangles. There are two such triangles – 1-2-3 and 4-5-6.
So the total number of triangles in the given figure = 21+24+2 = 47


